category theory for programmers 2

引き続きcategory theory for programmersを読んでいるので続き。

productとcoproduct

圏論の世界ではuniversal constructionという考え方があるらしい。ある圏の中の特定のobjectを指定したいときに、

コレコレという性質を満たすobjectの中で、
いちばんアレな性質にフィットしているもの

みたいなロジックで何かを選び出す・・と、本には書いてあるけど、ちょっと抽象的すぎるな。で、具体的な例がいくつかでてくる。

initial object

全てのobjectに対して、ちょうど1つのmorphismを持つようなobject

のことを、initial objectという。集合の圏 Setでは、空集合 Voidがそれにあたる。

Voidがinitial objectっつうのは分かりづらいよなぁ・・。定義域が空集合なので、引数を一個も取れないのに、任意の集合に向けた関数がちょうど1個だけ定義できる、ということを言っている。これは、我々が生活する世界の何かを写し取っているというよりは、論理構造上、そのように決めといた方が他との整合性が取れてよろしい、というご都合的なものなんじゃろうと理解。任意の\(x\)に対して\(x^0 = 1\)と決めとこう、みたいな。実際、定義域に何か値があるならば、その値に対する評価値を何にするかっつうのは、値域となる集合の要素数だけあるわけで、initial objectにはなれないね。

terminal object

全てのobjectから、ちょうど1つのmorphismが来るようなobject

のことを、terminal objectという。集合の圏 Setでは、シングルトン = 要素数1の集合がそれにあたる。このロジックには、不明確なところはない。

ところで、{1}, {2}, {3} ... {"a"}, {"b"} ... などなど、この定義だとterminal objectは無限個あることになる。そうすると、「特定のobjectを指定する」という要求を果たしてないように思える。が、圏論としては、ここの不定性は諦めていて(というかobjectの中身を見ないことにしている理論なので、これ以上は原理的に追えないのだろう)、 up to isomorphismでユニークに指定できれば良いということになっている（ひどい日本語だ）。実際、initial objectやterminal objectは、up to isomorphismでユニーク、つまり、全てのinitial (terminal) objectは、お互いにisomorphicであることが言える。

isomorphism

a, bがobjectで、f: a -> bとg: b -> aがmorphismとする。

f . g = id

g . f = id

上のような関係にあるとき、a,bをisomorphismという。

products

デカルト積の概念を一般化したもの。デカルト積って要するにタプルで、タプルの概念の中に、それを別の世界に一般化し得るような、より基礎的な何かがあるなんて想像しなかったです。タプルなんてモノが並んでるだけだよ。圏論はすごい。

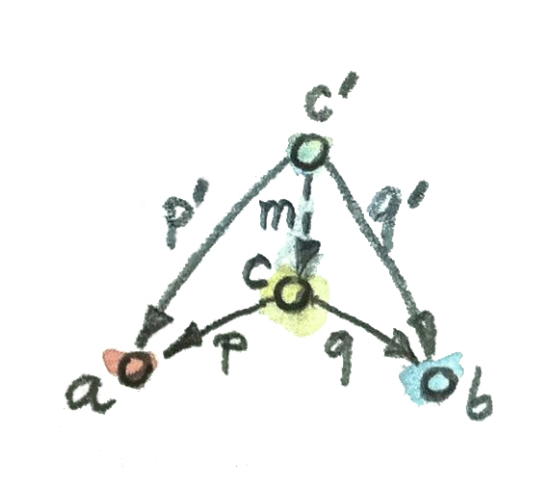
これから2つのobject aとbのproductと呼ばれるobject cを定義する。まず、第一の条件として、morphism p: c -> aとq: c -> bが存在する必要がある（コレコレという性質）。これだけだと、何でもありやんになってしまう。そこで、第二の条件として、c自身と、p, qに次のようなすごい特別な性質を要請する。

別のc'について、もし、morphism p': c' -> a, q': c' -> bが存在するならば、
morphism m: c' -> cが1つだけ存在して、次を満たす

p' = p . m

q' = q . m

いやー・・難しい。意味が分からない。圏論やばい。

抽象的な言葉の範囲で説明を書いておこう。詳しい説明は、テキストの5.5を読めば良い。集合の圏で考えると、実は、aとbのproduct cは、aとbのデカルト積 a x bで、p, qは、a, bそれぞれへの射影となる。上の定義での第二の要請は、

何かしらの集合からa or bに関数があったとき、まずmでa x bに情報を落としてから、a or bに射影しても良い。デカルト積なら、そういうことが必ずできる
何かしらの集合からa or bに関数があったとき、a x bより大きな集合に落としてからa or bに射影するとすると、そのような落とし方は無数にある（ので、「a x bより大きな集合」はデカルト積としてふさわしくない）

ということを言っている。

coproducts

直和型を一般化したもの。直和ってのは・・

\[A + B := (\{1\} \times A) \cup (\{2\} \times B)\]

無理やり数学で書くとこうなる。記号で見ると見づらいんだけど、つまり、\(A, B\)に共通要素があっても区別する和集合。 \(A=\{1, 2\}, B=\{2, 3\}\)のとき、\(|A\cup B|=3\)だけど、\(|A + B|=4\)。

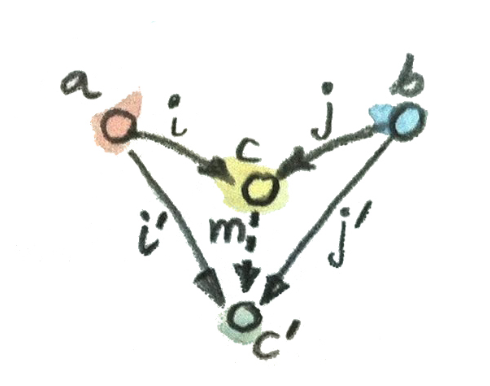
object a, bのcoproduct cを定義する。まず、第一の条件として、morphism i: a -> cとj: b -> cが存在する必要がある。で、例によってこれでは緩すぎるので、次のような絶妙な性質を要請する。

別のc'について、もし、morphism i': a -> c', j': b -> c'が存在するならば、
morphism m: c -> c'が1つだけ存在して、次を満たす

i' = m . i

j' = m . j

これは、productみたいに、普段使う数学の概念で説明するのは難しいなぁ。代わりにHaskellで考えよう。 Haskellでは、直和型はEitherである。で、上のi, jは、LeftとRightに相当する。そして、mは、次のように定義できる。

m :: (a -> c') -> (b -> c') -> Either a b -> c'
m i' _ (Left a) = i' a
m _ j' (Right b) = j' b

というのでも良いが、やっぱ分かった気にならないので、もう少し考えてみる。ここでのi, jは、要するにa, bからa+bへの埋め込みになっている、と思う。それを念頭に置いて、2通りのうまく行かない場合を考えてみよう。

cが狭すぎてダメな場合: cがシングルトンで、c’がa+bとする。i, jは自然に1個だけに定まる(cがシングルトンだから)。i’, j’として、埋め込みを考える。この場合、a, bの要素をi, jによってcの唯一の要素に移してしまうと、そのあとa+bの中から元のa, bの要素を復元することはできない。

cが広すぎてダメな場合: 適当な集合 dを持ってきて、c=a+b+dで、c’がa+b, i,jはa,bからa+b+dへの埋め込み、i’,j’として、a,bからa+bへの埋め込みを考える。この場合、m: c -> c’を定義するにあたって、dの要素をどこに移すかに自由度が残ってしまう。

というわけで、coproductの定義は、

a, bをcに埋め込んだあとに、さらに別の何かに埋め込むことができる (i' = m . i, j' = m . jという要請がそれ)
で、cは、そういうことができる最小の集合だ (そういうmが一個しか取れないという要請がそれ)

ということを言っているのだろう。

このあとの流れ

名前が示唆するとおりに、productは積っぽく振る舞う。で、実は、coproductは和っぽく振る舞う。さらに、terminal object, initial objectが、それぞれの単位元ぽく振る舞う。こっから代数的データ型とかの話になっていく。なんで、「代数的」なのかがやっと分かったよ。ある型と別の型のproduct / coproduct(=和)を作ることを繰り返して望みの型を定義するという世界なのでした。